Leetcode94.二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例 1：

inorder_1

1
2
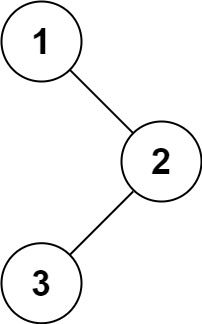
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

1
2
输入：root = []
输出：[]

示例 3：

1
2
输入：root = [1]
输出：[1]

提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

解法1：递归

直接使用递归进行操作比较简单，但是同样地也会消耗较多资源

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> temp = new ArrayList<Integer>();
        inorder(root,temp);
        return temp;
    }

    public void inorder(TreeNode node, List<Integer> res){
        if (node == null){
            return;
        }
        inorder(node.left,res);
        res.add(node.val);
        inorder(node.right,res);
    }
}

解法2：迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        Deque<TreeNode> stack = new LinkedList<TreeNode>();

        while (!stack.isEmpty() || root != null){
            while(root != null){
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            res.add(root.val);
            root = root.right;
        } 
        return res;

    }
}

解法3：Morris遍历

使用Morris遍历能够将时间复杂度降到O(1),由于每个节点都访问了两次，所以空间复杂度为O(2n) = O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        TreeNode pre = null;
        List<Integer> res = new ArrayList<Integer>();
        while (root!=null){
            if (root.left != null){
                pre = root.left;
                while(pre.right != null && pre.right != root){
                    pre = pre.right;
                }


                if (pre.right == null){
                    pre.right = root;
                    root = root.left;
                }else{
                    res.add(root.val);
                    pre.right = null;
                    root = root.right;
                }
            }else{
                res.add(root.val);
                root = root.right;
            }
        }
        return res;
    }
}